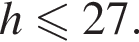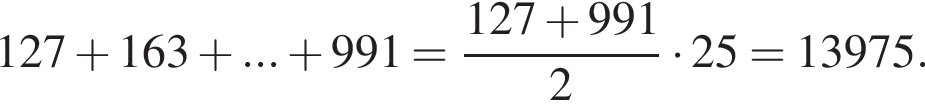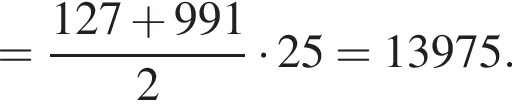На координатной прямой отмечены точки А, В, С, D, F. Числу ![]() на координатной прямой может соответствовать точка:
на координатной прямой может соответствовать точка:
На клетчатой бумаге с клетками размером 1 см х 1 см изображён параллелограмм. Найдите его площадь в квадратных сантиметрах.
Прямые a и b, пересекаясь, образуют четыре угла. Известно, что сумма трех углов равна 200°. Найдите градусную меру меньшего угла.
Найдите значение выражения 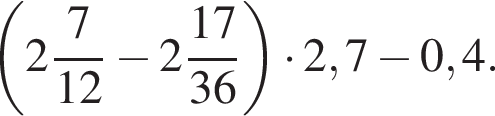
Вычислите 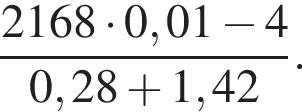
Результат упрощения выражения 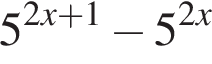 имеет вид:
имеет вид:
Точки A, B, C разделили окружность так, что градусные меры дуг AB, BC, CA в указанном порядке находятся в отношении 5 : 6 : 7. Найдите градусную меру угла ABC.
Вычислите 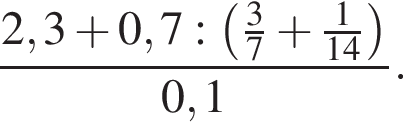
От пристани одновременно отправляются по течению реки катер(I) и против течения реки моторная лодка (II). На рисунке приведены графики их движения. Определите скорость течения реки (в км/ч), если катер и моторная лодка имеют одинаковые собственные скорости.
Прямая a пересекает плоскость α в точке A и образует с плоскостью угол 60°. Точка B лежит на прямой a, причем AB = ![]() Найдите расстояние от точки B до плоскости α.
Найдите расстояние от точки B до плоскости α.
Упростите выражение 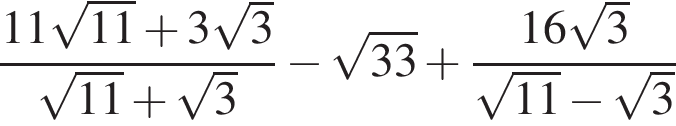
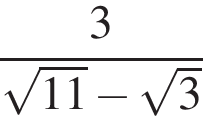
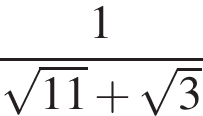
Укажите номер рисунка, на котором представлен эскиз графика функции y = 1 − (x + 3)2.
Найдите значение выражения 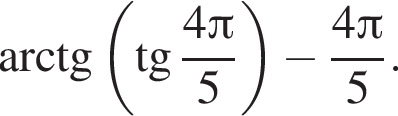
Известно, что наименьшее значение функции, заданной формулой y = x2 + 8x + c, равно −3. Тогда значение c равно:
Корень уравнения 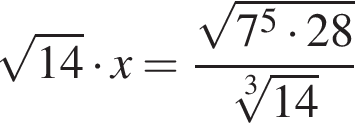 равен:
равен:
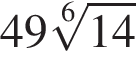
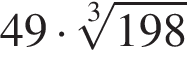
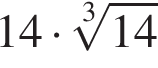
Из полного бокала, имеющего форму конуса высотой 9, отлили треть (по объему) жидкости. Вычислите ![]() где h — высота оставшейся жидкости.
где h — высота оставшейся жидкости.
Через вершину A прямоугольного треугольника ABC (∠C = 90°) проведен перпендикуляр AK к его плоскости. Найдите расстояние от точки K до прямой BC, если AK = 2, AB = 4, BC = ![]()
Сумма всех натуральных решений неравенства 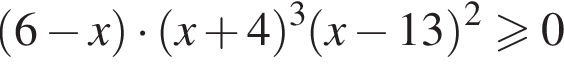 равна:
равна:
Если в правильной четырехугольной пирамиде высота равна 4, а площадь диагонального сечения равна 12, то ее объем равен ...
Найдите произведение большего корня на количество корней уравнения 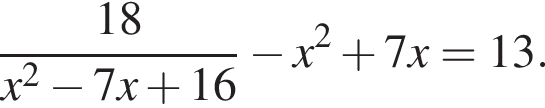
Основание остроугольного равнобедренного треугольника равно 2, а синус противоположного основанию угла равен 0,8. Найдите площадь треугольника.
Найдите периметр правильного шестиугольника, меньшая диагональ которого равна ![]()
Найдите наибольшее целое решение неравенства 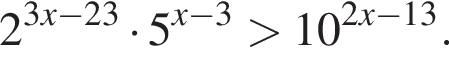
Найдите
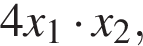 где x1, x2 — абсциссы точек пересечения параболы и горизонтальной прямой (см. рис.).
где x1, x2 — абсциссы точек пересечения параболы и горизонтальной прямой (см. рис.).
Каждое боковое ребро четырехугольной пирамиды образует с ее высотой, равной ![]() угол 30°. Основанием пирамиды является прямоугольник с углом 30° между диагоналями. Найдите объем пирамиды V, в ответ запишите значение выражения
угол 30°. Основанием пирамиды является прямоугольник с углом 30° между диагоналями. Найдите объем пирамиды V, в ответ запишите значение выражения ![]()
Найдите значение выражения 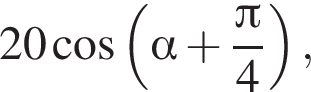 если
если 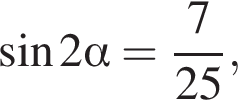
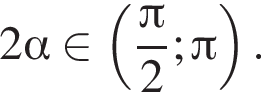
Из города А в город В, расстояние между которыми 100 км, одновременно выезжают два автомобиля. Скорость первого автомобиля на 10 км/ч больше скорости второго, но он делает в пути остановку на 50 мин. Найдите наибольшее значение скорости (в км/ч) первого автомобиля, при движении с которой он прибудет в В не позже второго.
Найдите произведение наименьшего и наибольшего целых решений неравенства 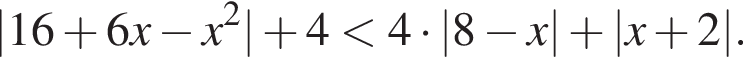
Если 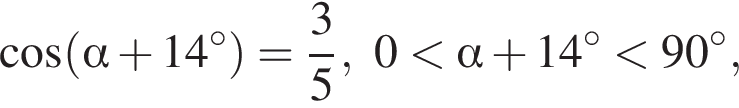 то значение выражения
то значение выражения 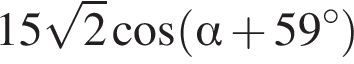 равно ...
равно ...
Найдите сумму всех трехзначных чисел, которые при делении на 4 дают в остатке 3, а при делении на 6 и на 9 дают в остатке 1.

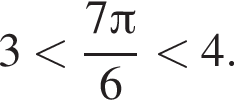 Таким образом, точка D может соответствовать этому числу.
Таким образом, точка D может соответствовать этому числу.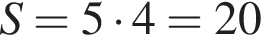 см2.
см2. равна 360°, поэтому четвертый угол равен 160°. Углы 1 и 3, 2 и 4 — вертикальные, следовательно, они равны. Смежные углы в сумме 180°, следовательно, меньший угол равен 20°.
равна 360°, поэтому четвертый угол равен 160°. Углы 1 и 3, 2 и 4 — вертикальные, следовательно, они равны. Смежные углы в сумме 180°, следовательно, меньший угол равен 20°.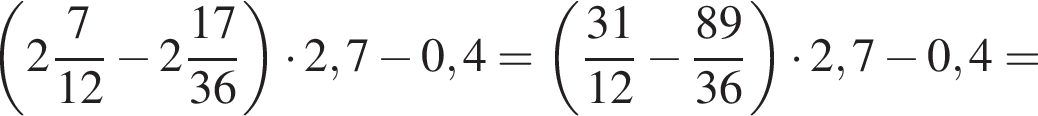
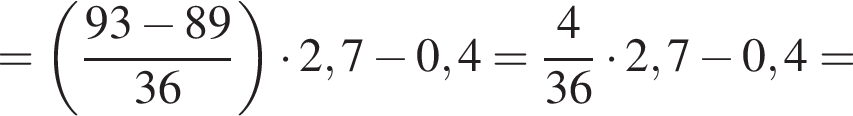
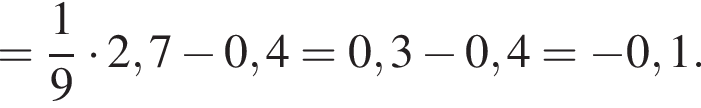
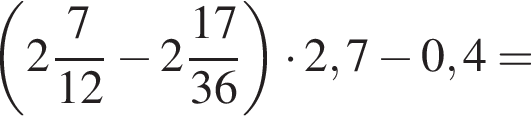
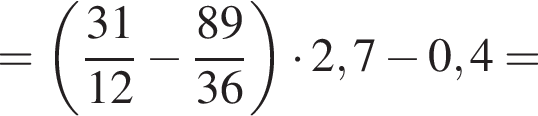
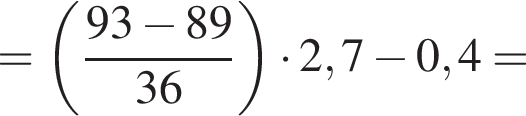
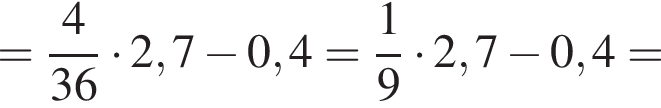
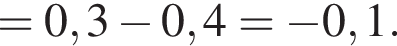
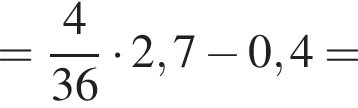
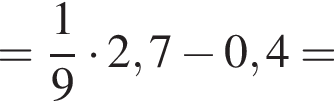
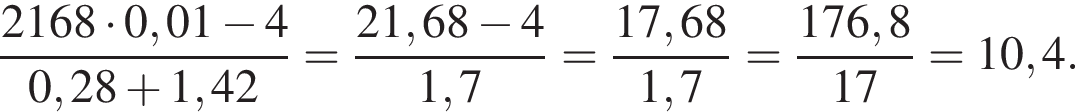
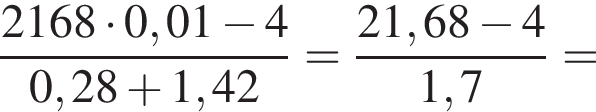
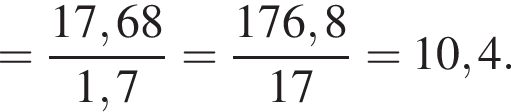
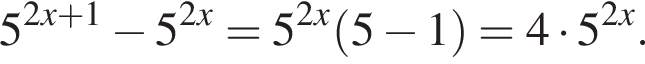
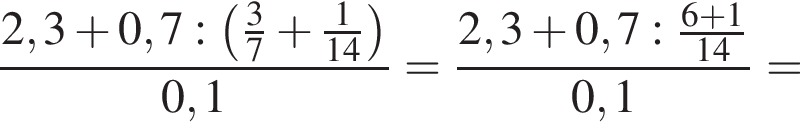
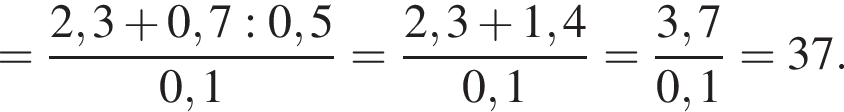
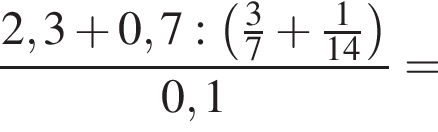
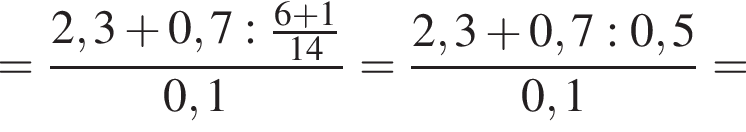
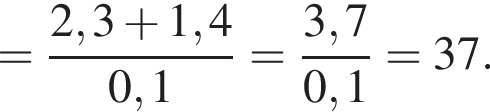
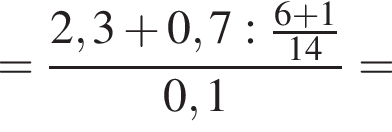
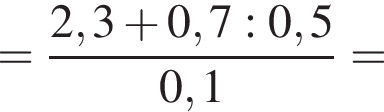
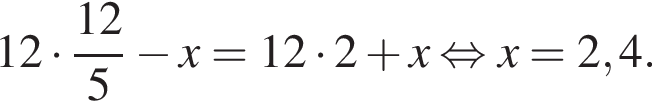

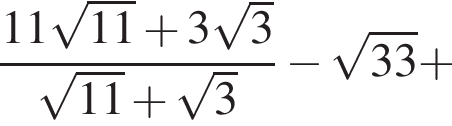
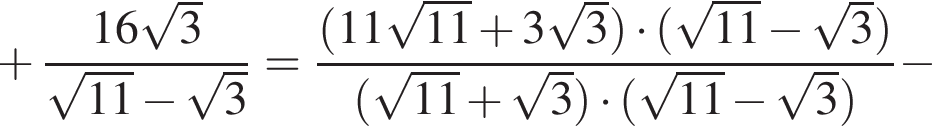
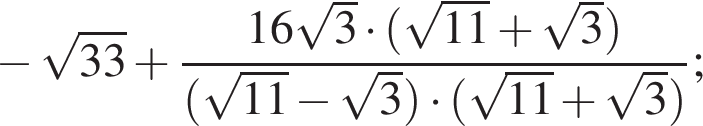

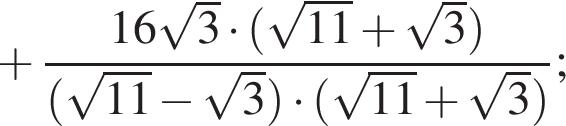
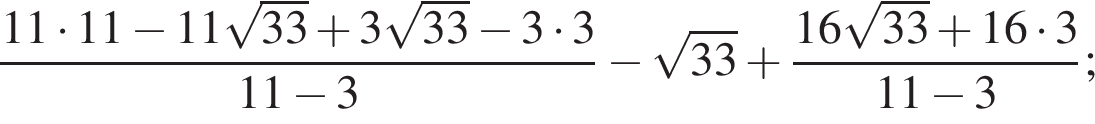
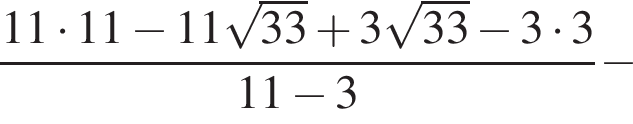
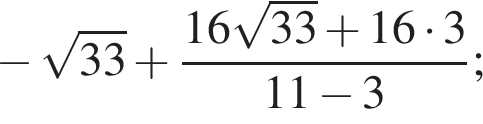
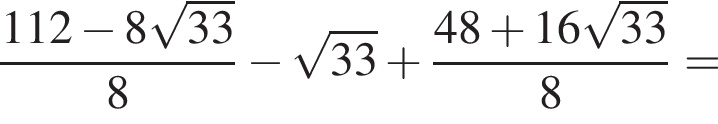
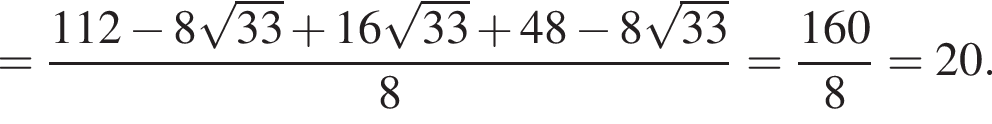
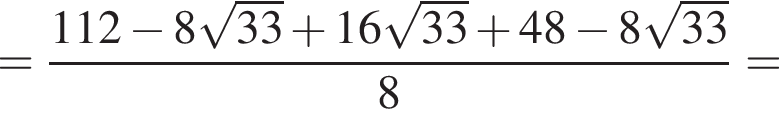
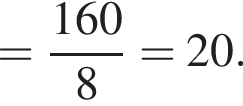
 только для
только для 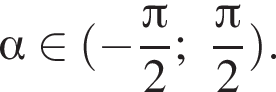 Поэтому преобразуем, используя формулы приведения:
Поэтому преобразуем, используя формулы приведения: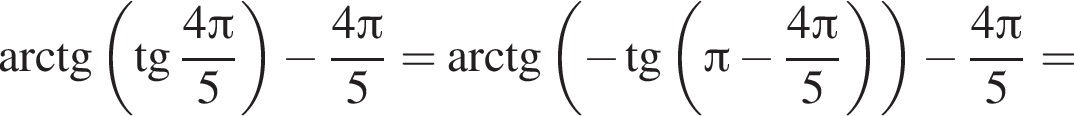
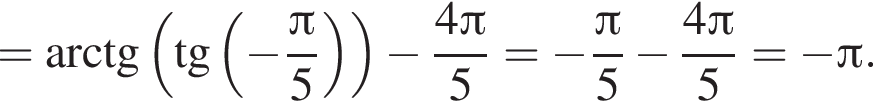
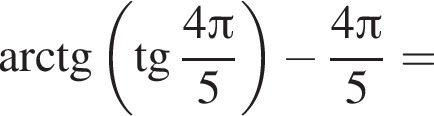
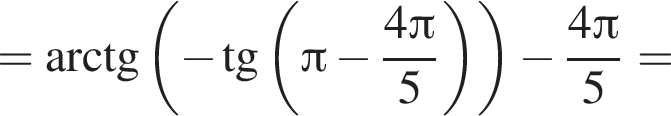
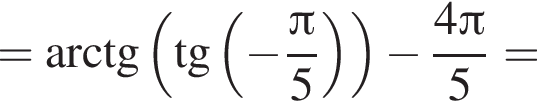
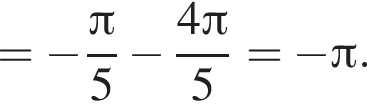
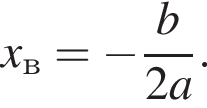 Поэтому
Поэтому 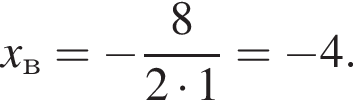 Поскольку y(xв) = −3, имеем:
Поскольку y(xв) = −3, имеем: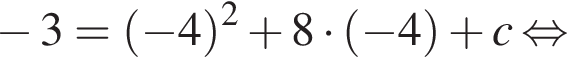

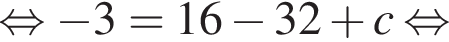
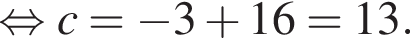
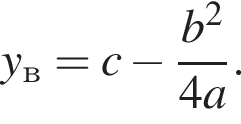
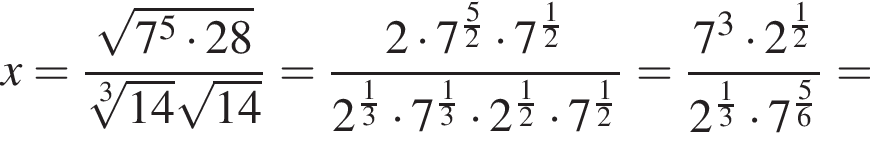
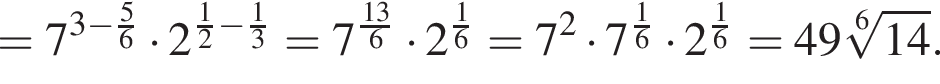
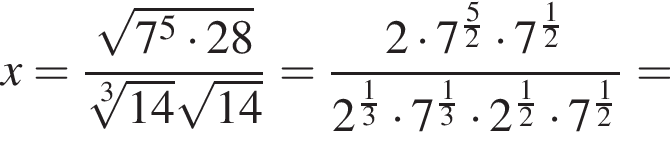
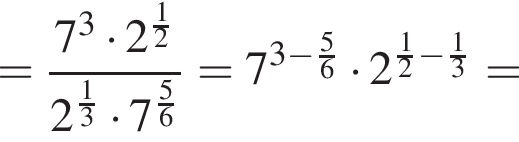
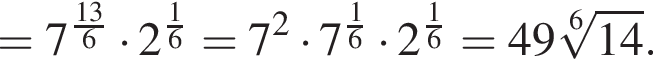
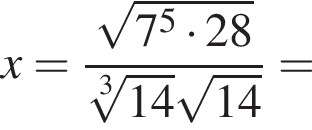
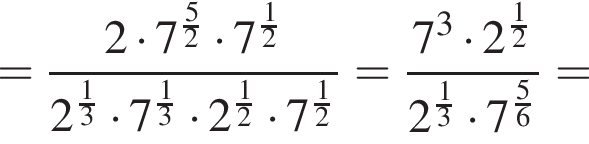
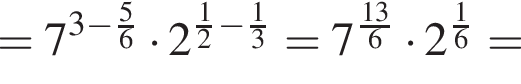
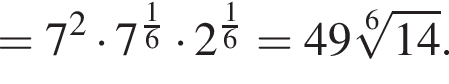
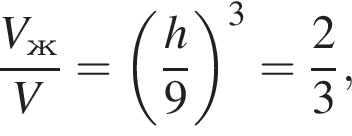 откуда
откуда 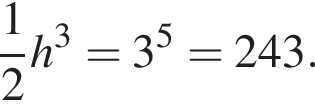
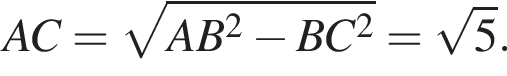 Заметим, что AC является проекцией наклонной KC на плоскость ABC и AC
Заметим, что AC является проекцией наклонной KC на плоскость ABC и AC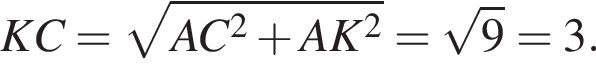
 и при
и при 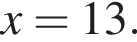 Натуральными решениями являются числа 1, 2, 3, 4, 5, 6, 13. Их сумма равна 34.
Натуральными решениями являются числа 1, 2, 3, 4, 5, 6, 13. Их сумма равна 34.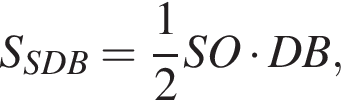 следовательно,
следовательно, 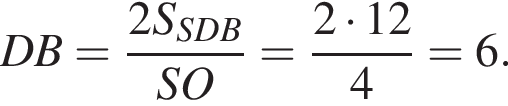
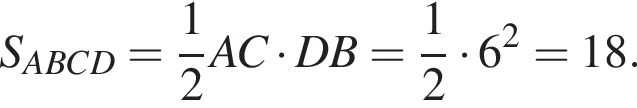 Следовательно,
Следовательно,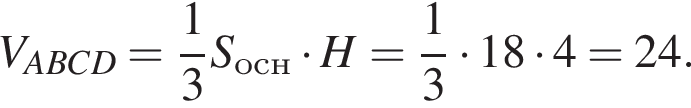
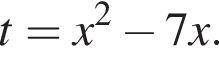 Тогда:
Тогда: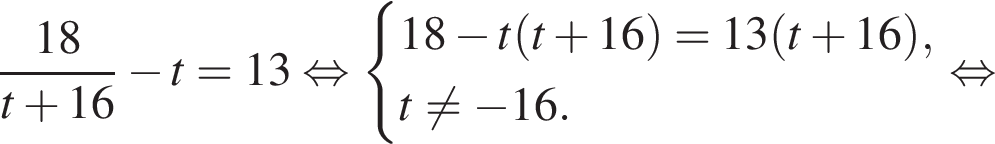
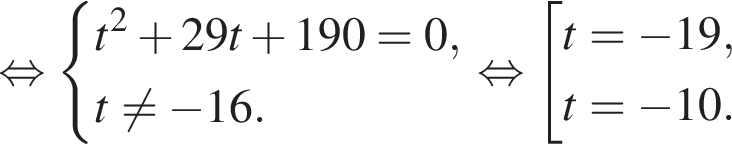
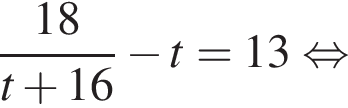
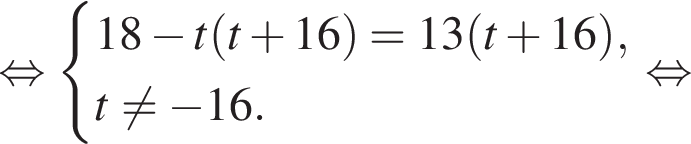
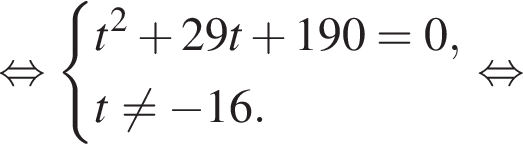

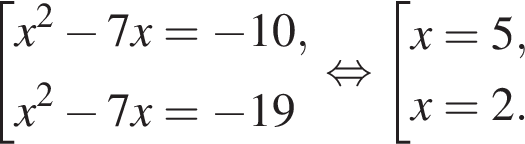
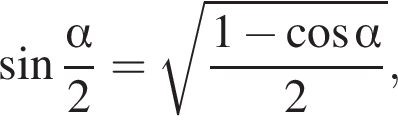 где
где 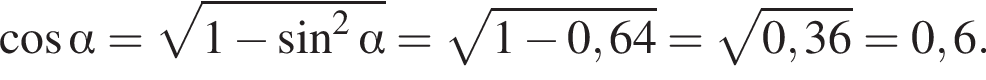
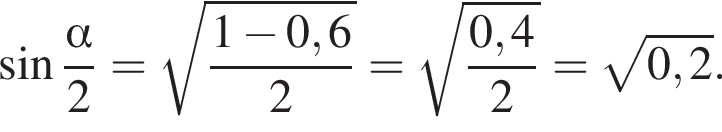
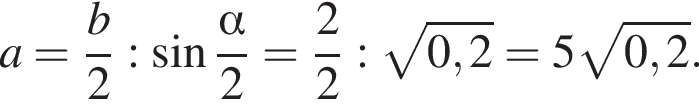
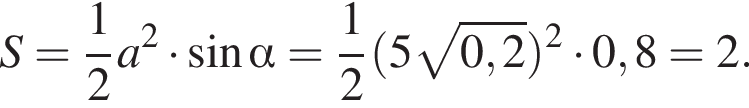
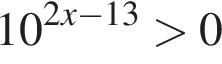 :
: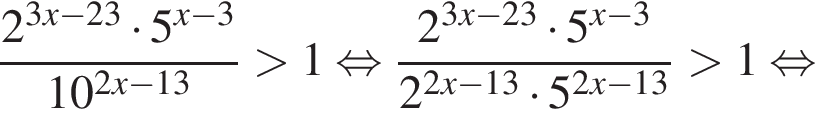
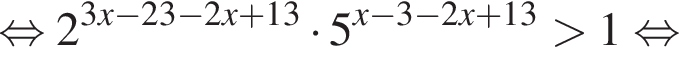
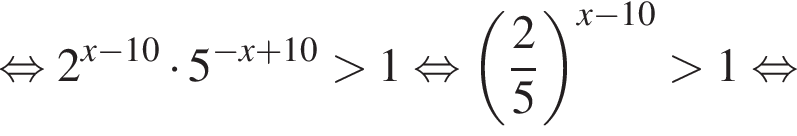
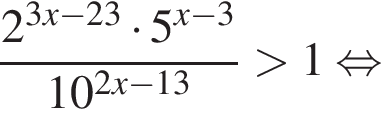
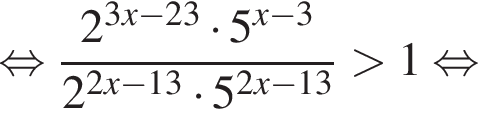
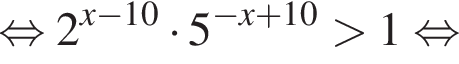
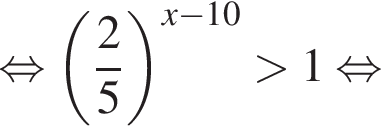

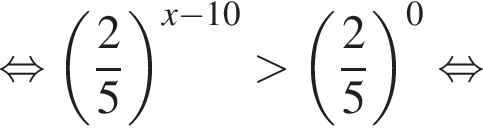
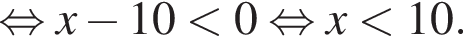
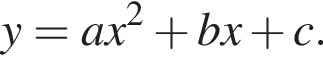 На рисунке изображена парабола с ветвями, направленными вверх, следовательно,
На рисунке изображена парабола с ветвями, направленными вверх, следовательно, 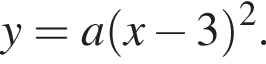 Для того, чтобы найти a, подставим в уравнение параболы точку (2;1), через которую данная парабола проходит:
Для того, чтобы найти a, подставим в уравнение параболы точку (2;1), через которую данная парабола проходит: 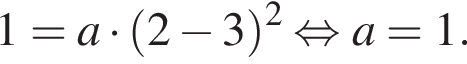 Таким образом, изображённая на графике парабола задается уравнением
Таким образом, изображённая на графике парабола задается уравнением 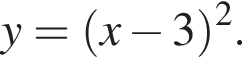
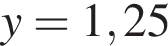 :
: 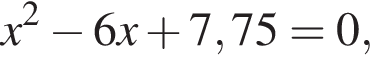 откуда по теореме Виета
откуда по теореме Виета 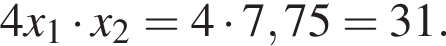
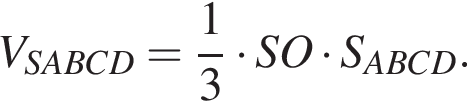 Площадь прямоугольника можно найти как полупроизведение диагоналей d на синус угла между ними
Площадь прямоугольника можно найти как полупроизведение диагоналей d на синус угла между ними 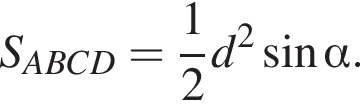 Из прямоугольного треугольника SOA найдем половину диагонали основания:
Из прямоугольного треугольника SOA найдем половину диагонали основания: 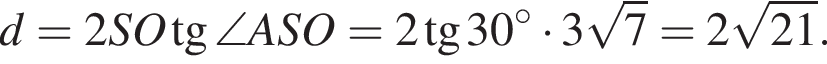
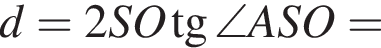

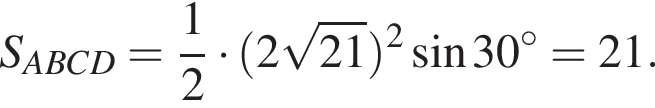 Тогда объём пирамиды равен:
Тогда объём пирамиды равен: 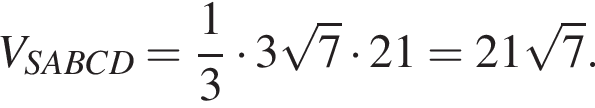 Поэтому
Поэтому 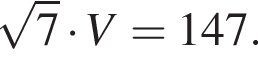
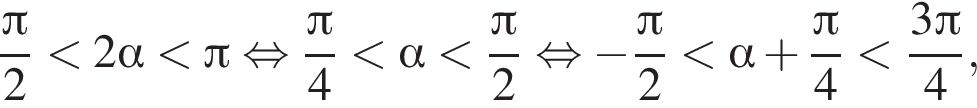

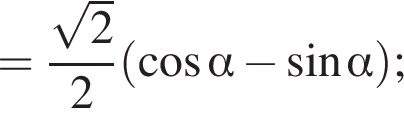
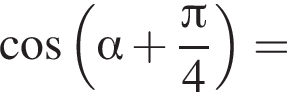
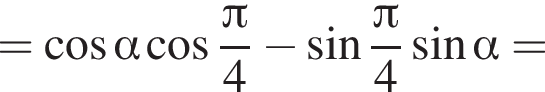
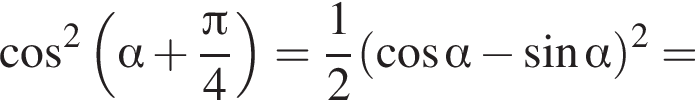

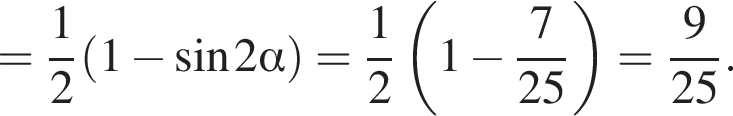
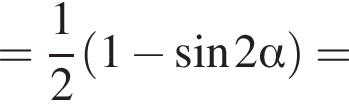
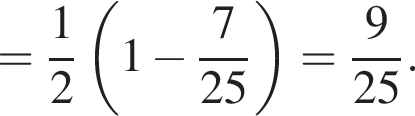
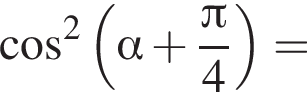
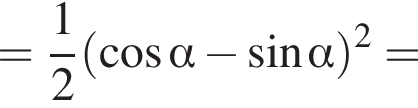
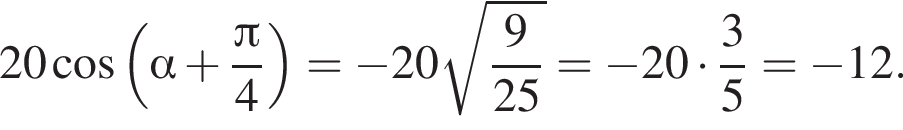
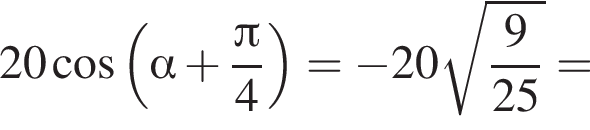
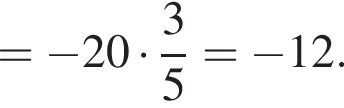
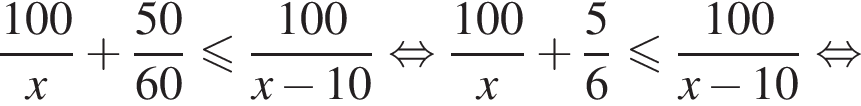

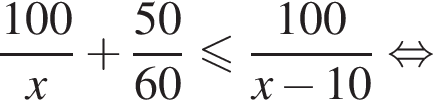
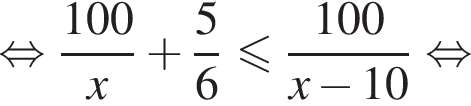
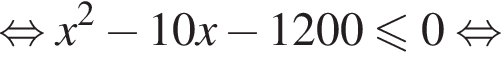

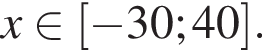 Таким образом, наибольшее значение скорости первого автомобиля — 40 км/ч.
Таким образом, наибольшее значение скорости первого автомобиля — 40 км/ч. имеем:
имеем: 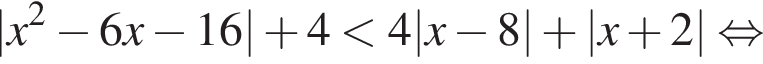
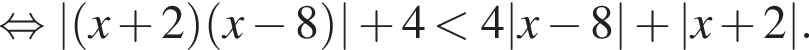
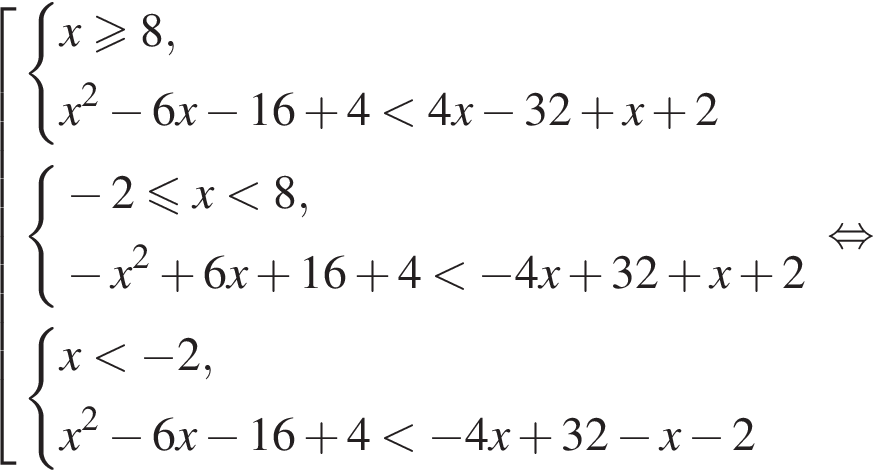
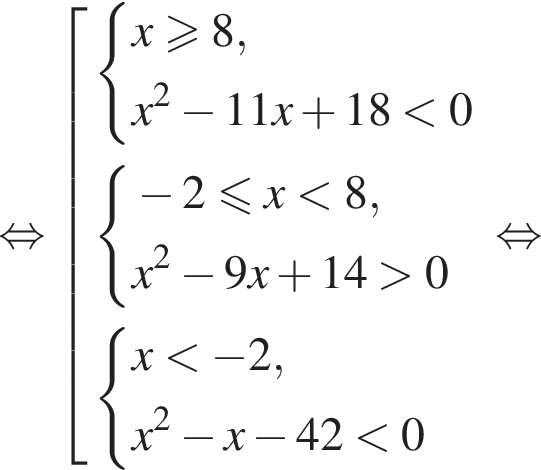

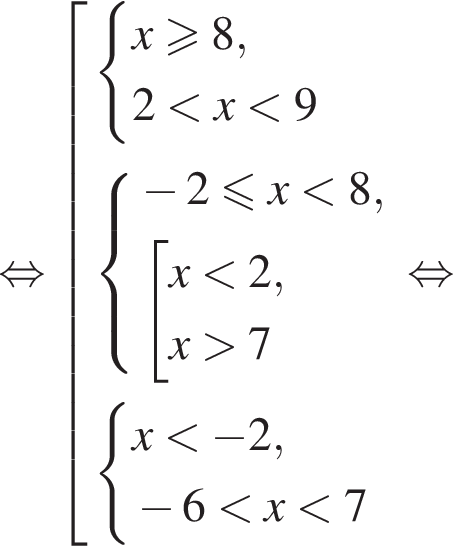
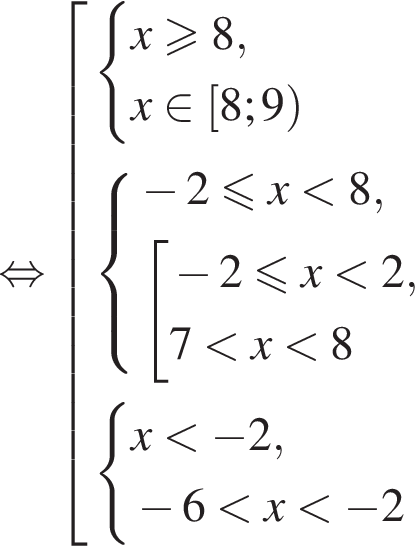
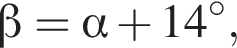 следовательно,
следовательно, 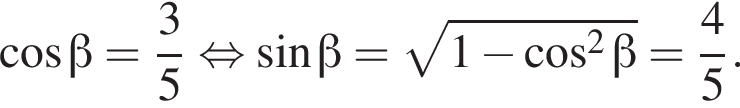 Заметим, что
Заметим, что  Таким образом:
Таким образом: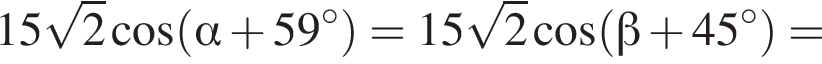
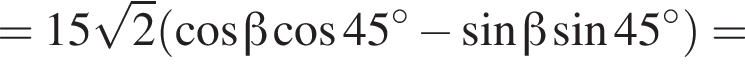
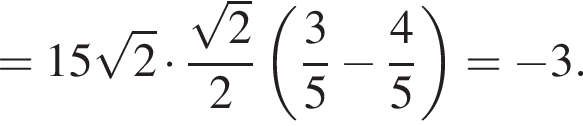
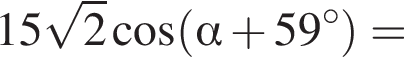
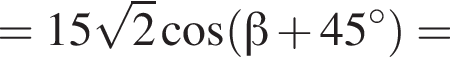
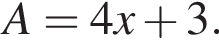


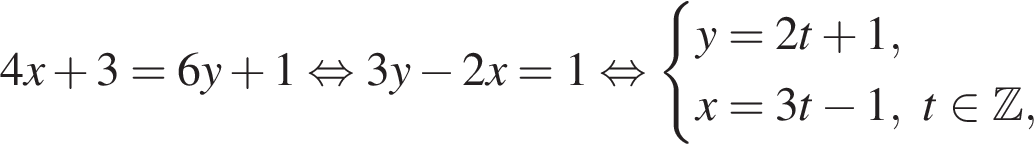
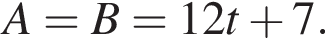
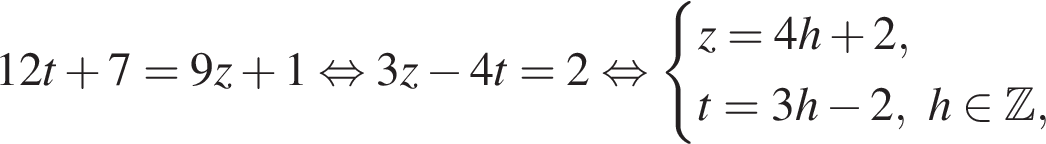

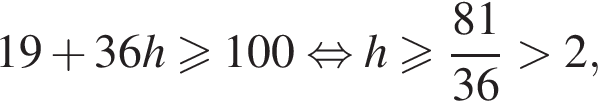 h — целое, поэтому
h — целое, поэтому  h — целое, поэтому
h — целое, поэтому